主要适用对象
Edexcel FP1考生
AQA FPSM1考生
CIE FP1、FP2考生
前言
矩阵是什么?矩阵从何而来?为什么矩阵中的运算及相关定义是那么突然,但却合理?我们相信会有一部分人在学习过程中感到不解,但却又带着这种疑惑接受了既定事实并做对了题目. 我们希望能在这一篇文章中尽可能解释清楚一些在教学中遇到的常见问题,帮助考生进一步理解矩阵.
矩阵
矩阵并不是凭空出现的. 解方程是古典代数学研究的重要问题,其中$n$个未知量的一次方程构成的方程组称为$n$元线性方程组. 在研究$n$元线性方程组的解法过程中,矩阵的概念就自然而然地出现了:考虑$m$个方程构成的$n$元线性方程组,未知量所对应的系数共$mn$个,常数项共$m$个. 若只考虑未知量系数,则由$mn$个数排成的$m$行、$n$列的一张表称为一个$m \times n$矩阵(又称系数矩阵,Coefficient Matrix). 若同时考虑未知量系数与常数项,则由$m(n+1)$个数排成的$m$行、$n+1$列的一张表称为$m \times (n+1)$矩阵(又称增广矩阵,Augmented Matrix). 随着学科的发展,矩阵这一工具也不断发展,这就是后话了.
说明:增广矩阵的概念仅出现在CIE教材中,可用于解方程组.
行列式(Determinant)
尽管在爱德思(Edexcel)、AQA和CIE教材中都是先定义矩阵,再定义行列式,但历史上恰好相反,矩阵正式作为数学中的研究对象是在行列式的研究发展之后. 考虑一个两个方程的二元一次方程组:
$$\begin{cases}
a_{11}x_1+a_{12}x_2=c_1 \\
a_{21}x_1+a_{22}x_2=c_2
\end{cases}$$
上述方程组的解为:
$$\begin{aligned}
x_1=\frac{c_1a_{22}-c_2a_{12}}{a_{11}a_{22}-a_{12}a_{21}},\ x_2=\frac{a_{11}c_2-a_{21}c_1}{a_{11}a_{22}-a_{12}a_{21}}
\end{aligned}$$
观察发现,上述方程组有唯一解当且仅当$a_{11}a_{22}-a_{12}a_{21} \neq 0$. 若$a_{11}a_{22}-a_{12}a_{21}=0$,上述方程组无解或有无穷多个解.
为了便于记忆表达式$a_{11}a_{22}-a_{12}a_{21}$,将其记为
$$\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}$$
这个表达式称为二阶行列式,也正是上述方程组对应的系数矩阵
$$A=\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}$$
的行列式,记为$|A|$或$\det(A)$. 因此,上述方程组有唯一解当且仅当$\det(A) \neq 0$.
幸运的是,当我们妥善定义$n$阶行列式后,$n$个方程的$n$元线性方程组也有类似的结论——方程组有唯一解当且仅当$\det(A) \neq 0$.
矩阵的运算
矩阵加法
表格是一种常用的数据可视化方式,表格结构简单,便于浏览和获取信息. 矩阵作为一种表格也具有同样的特点. 考虑三位巫师在2023年上半年与2023年下半年的咒语使用情况,如下表所示:
|
召唤咒 |
悬浮咒 |
照明咒 |
| 哈利·波特 |
5 |
3 |
1 |
| 赫敏·格兰杰 |
4 |
3 |
6 |
| 罗恩·韦斯莱 |
3 |
4 |
2 |
|
召唤咒 |
悬浮咒 |
照明咒 |
| 哈利·波特 |
2 |
0 |
8 |
| 赫敏·格兰杰 |
6 |
5 |
11 |
| 罗恩·韦斯莱 |
0 |
3 |
2 |
我们想分析三位巫师在2023年的咒语使用情况,只需要将对应巫师及咒语的使用次数相加即可. 这一过程就是矩阵的加法:
$$\begin{pmatrix}
5 & 3 & 1 \\
4 & 3 & 6 \\
3 & 4 & 2
\end{pmatrix} + \begin{pmatrix}
2 & 0 & 8 \\
6 & 5 & 11 \\
0 & 3 & 2
\end{pmatrix} = \begin{pmatrix}
7 & 3 & 9 \\
10 & 8 & 17 \\
3 & 7 & 4
\end{pmatrix}$$
只有两个矩阵形状相同(均为$n$行$m$列),矩阵加法才有意义,且是对应位置的元素相加. 不难理解,矩阵加法具有交换律与结合律.
矩阵数乘
矩阵数乘也很好理解,比如同步增长的经济问题很自然地引出矩阵的数量乘法运算,$kA$意味着矩阵中的所有元素乘上$k$.
矩阵乘法
教材介绍了矩阵乘法的计算规则,我们提供不同的角度去理解矩阵乘法. 首先回到线性方程组:
$$\begin{cases}
8x_1+2x_2=11 \\
2x_1+5x_2=9
\end{cases}$$
矩阵可以为上述线性方程组提供一个简便的形式:
$$\begin{pmatrix}
8 & 2 \\
2 & 5
\end{pmatrix}\begin{pmatrix}
x_1 \\
x_2
\end{pmatrix} = \begin{pmatrix}
11 \\
9
\end{pmatrix}$$
结合矩阵形式与线性方程组,已经能看出矩阵乘法($2 \times 2$矩阵与$2 \times 1$向量相乘)的计算规则,但我们需要进一步探究. 考虑下列两组线性方程组:
$$\begin{cases}
a_{11}x_1+a_{12}x_2=y_1 \\
a_{21}x_1+a_{22}x_2=y_2
\end{cases} \ \ \text{与}\ \ \begin{cases}
b_{11}t_1+b_{12}t_2=x_1 \\
b_{21}t_1+b_{22}t_2=x_2
\end{cases}$$
矩阵写法为:
$$\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}\begin{pmatrix}
x_1 \\
x_2
\end{pmatrix}=\begin{pmatrix}
y_1 \\
y_2
\end{pmatrix} \ \ \text{与}\ \ \begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}\begin{pmatrix}
t_1 \\
t_2
\end{pmatrix}=\begin{pmatrix}
x_1 \\
x_2
\end{pmatrix}$$
合并两个方程组后可得:
$$\begin{cases}
a_{11}(b_{11}t_1+b_{12}t_2)+a_{12}(b_{21}t_1+b_{22}t_2)=y_1 \\
a_{21}(b_{11}t_1+b_{12}t_2)+a_{22}(b_{21}t_1+b_{22}t_2)=y_2
\end{cases}$$
即:
$$\begin{cases}
(a_{11}b_{11}+a_{12}b_{21})t_1+(a_{11}b_{12}+a_{12}b_{22})t_2=y_1 \\
(a_{21}b_{11}+a_{22}b_{21})t_1+(a_{21}b_{12}+a_{22}b_{22})t_2=y_2
\end{cases}$$
同理,矩阵可以变为:
$$\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}\begin{pmatrix}
t_1 \\
t_2
\end{pmatrix}=\begin{pmatrix}
y_1 \\
y_2
\end{pmatrix}$$
因此
$$\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}=\begin{pmatrix}
a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} \\
a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22}
\end{pmatrix}$$
也就是我们熟悉的矩阵乘法计算规则.
我们再来看一个更加直观的几何例子.
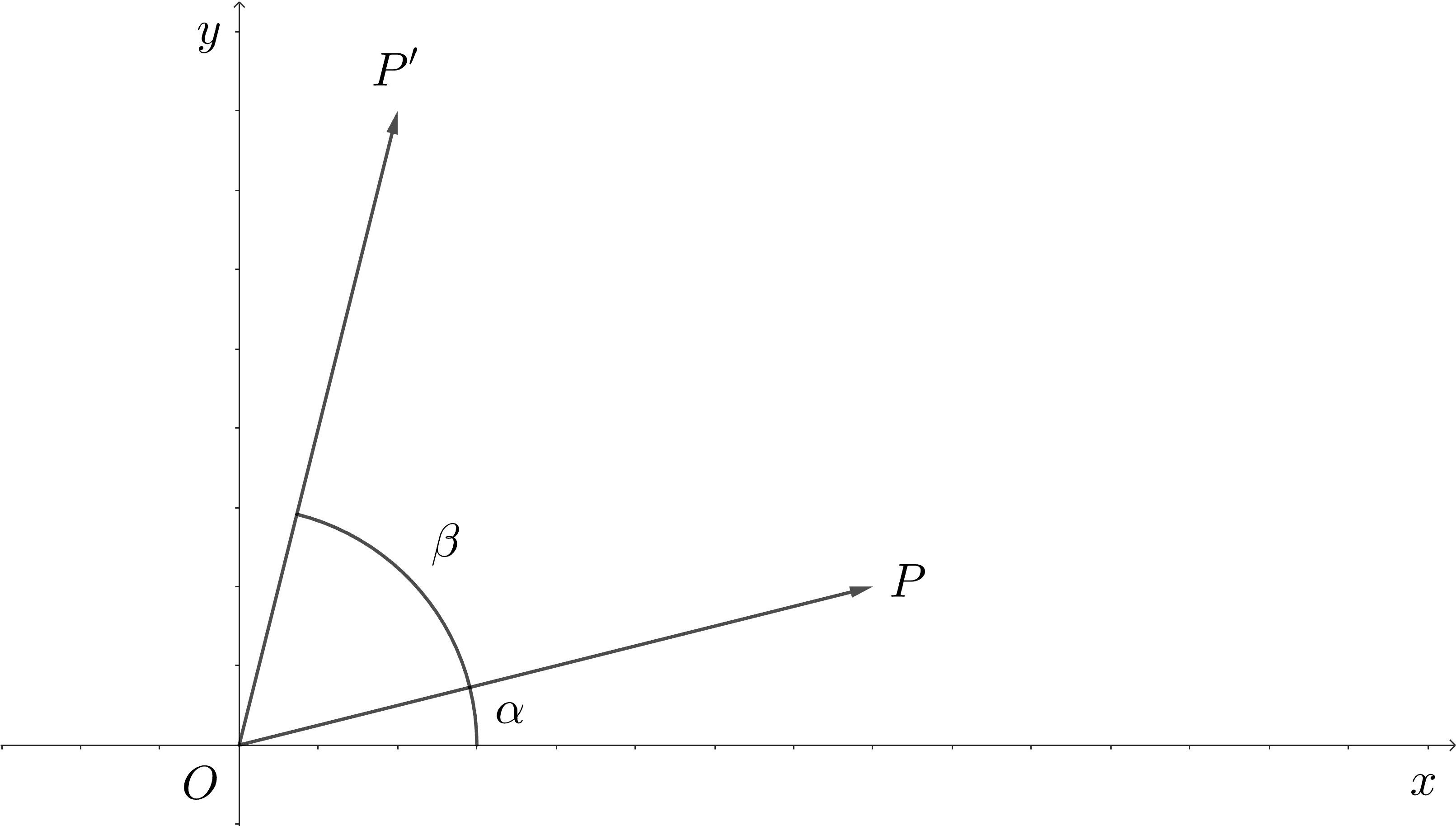
假设点$P(x, y)$围绕原点$O$逆时针旋转$\beta$后到点$P'(x', y')$. 假设$OP$长度为$r$,根据三角函数的定义可得
$$
x=r\cos\alpha \\
y=r\sin\alpha \\
x'=r\cos(\alpha+\beta) \\
y'=r\sin(\alpha+\beta)
$$
根据三角函数相关公式
$$
x'=r\cos(\alpha+\beta)=r\cos\alpha\cos\beta-r\sin\alpha\sin\beta=x\cos\beta-y\sin\beta \\
y'=r\sin(\alpha+\beta)=r\sin\alpha\cos\beta+r\cos\alpha\sin\beta=x\sin\beta+y\cos\beta
$$
矩阵写法为:
$$\begin{pmatrix}
\cos\beta & -\sin\beta \\
\sin\beta & \cos\beta
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix} = \begin{pmatrix}
x' \\
y'
\end{pmatrix}$$
因此,矩阵$\displaystyle \begin{pmatrix}
\cos\beta & -\sin\beta \\
\sin\beta & \cos\beta
\end{pmatrix}$用于表示围绕原点$O$逆时针旋转$\beta$——anticlockwise rotation through $\beta$ about $O$.
Surprise!
从这个例子中,我们惊喜地发现矩阵与几何的联系. 在爱德思、AQA与CIE的教材中,我们探讨了线性变换(Linear Transformation),即可以用矩阵表示的变换. 在数学中,线性变换亦可称为线性映射(Linear Mapping). 不严谨地说(为了理解),我们可以将矩阵视为一个“函数”,输入点$P$经过“矩阵函数”的作用后得到输出点$P'$:
$$
\begin{pmatrix}
x \\
y
\end{pmatrix} \xrightarrow[]{\begin{pmatrix}
\cos\beta & -\sin\beta \\
\sin\beta & \cos\beta
\end{pmatrix}} \begin{pmatrix}
x' \\
y'
\end{pmatrix}
$$
不妨再假设点$P'(x', y')$围绕原点$O$逆时针旋转$\theta$后到点$P''(x'', y'')$. 从点$P$围绕原点$O$逆时针旋转到点$P''$,我们可以从两个角度思考:
1. 点$P$围绕原点$O$逆时针旋转$\beta+\theta$后到点$P''$.
2. 点$P$围绕原点$O$逆时针旋转$\beta$后到点$P'$,再由点$P'$围绕原点$O$逆时针旋转$\theta$后到点$P''$.
从第一个角度来看,可以用矩阵表示为
$$\begin{aligned}
&\begin{pmatrix}
\cos(\beta+\theta) & -\sin(\beta+\theta) \\
\sin(\beta+\theta) & \cos(\beta+\theta)
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix} = \begin{pmatrix}
x'' \\
y''
\end{pmatrix} \\
\Rightarrow &\begin{pmatrix}
\cos\beta\cos\theta-\sin\beta\sin\theta & -\sin\beta\cos\theta-\cos\beta\sin\theta \\
\sin\beta\cos\theta+\cos\beta\sin\theta & \cos\beta\cos\theta-\sin\beta\sin\theta
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix} = \begin{pmatrix}
x'' \\
y''
\end{pmatrix}
\end{aligned}$$
从第二个角度来看,
$$
\begin{pmatrix}
x \\
y
\end{pmatrix} \xrightarrow[]{\begin{pmatrix}
\cos\beta & -\sin\beta \\
\sin\beta & \cos\beta
\end{pmatrix}} \begin{pmatrix}
x' \\
y'
\end{pmatrix} \xrightarrow[]{\begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{pmatrix}} \begin{pmatrix}
x'' \\
y''
\end{pmatrix}
$$
可以用矩阵表示为
$$\begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{pmatrix}\begin{pmatrix}
\cos\beta & -\sin\beta \\
\sin\beta & \cos\beta
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix} = \begin{pmatrix}
x'' \\
y''
\end{pmatrix}$$
因此
$$
\begin{aligned}
\begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{pmatrix}\begin{pmatrix}
\cos\beta & -\sin\beta \\
\sin\beta & \cos\beta
\end{pmatrix}&=\begin{pmatrix}
\cos\beta\cos\theta-\sin\beta\sin\theta & -\sin\beta\cos\theta-\cos\beta\sin\theta \\
\sin\beta\cos\theta+\cos\beta\sin\theta & \cos\beta\cos\theta-\sin\beta\sin\theta
\end{pmatrix} \\
&=\begin{pmatrix}
\cos\theta\cos\beta-\sin\theta\sin\beta & -\cos\theta\sin\beta-\sin\theta\cos\beta \\
\sin\theta\cos\beta+\cos\theta\sin\beta & -\sin\theta\sin\beta+\cos\theta\cos\beta
\end{pmatrix}
\end{aligned}
$$
也是我们熟悉的矩阵乘法计算规则.
根据多个具有实际意义的例子,我们可以妥善定义矩阵乘法.
总结
考生应优先掌握矩阵的基本运算,本文希望能帮助学有余力的考生进一步理解矩阵. 数学概念譬如矩阵并不是凭空出现的,我们观察客观世界的现象,抓住主要特征,抽象出其概念或者建立模型,并进一步深入分析与论证. 矩阵乘法就是一个很好的例子,我们为了解决多个类似问题,抽象出矩阵乘法计算规则,并适用于所有类似问题. 数学是自然且优美的,希望这篇文章能让各位考生感受数学之美,也希望各位考生能在未来保持探索数学的热情.


