比较数据（Compare Data）

主要适用对象

Edexcel S1考生

CIE S1考生

知识点介绍

比较数据一般从两个角度进行比较：

1. 集中趋势（Measure of Central Tendency）

(1) 常用于比较的指标：中位数（Median）、平均数（Mean）.
(2) 描述模版：比较指标，the average of (something) is higher/lower than that of (something).

2. 离散程度（Measure of Spread/Variation）

(1) 常用于比较的指标： 极差（Range）、四分位距（Interquartile Range/IQR）、方差（Variance）、标准差（Standard Deviation）.
(2) 描述模版：比较指标，(something) is more/less variable (or spread out) than (something).

一般我们同时使用中位数和IQR来比较数据，或者同时使用平均数和方差（或标准差）来比较数据. 前者的优点是不容易受到极端值的影响.

比较数据

集中趋势和离散程度是描述数据分布（Distribution）最常用的两个性质，集中趋势表明数据的平均水平，离散程度表明数据的波动程度. 需要注意的是，波动程度和稳定性是联系在一起的：数据波动程度越大，越不稳定；数据波动程度越小，越稳定. 如果考察到比较数据的题型，一般比较直接，只需要算出指标的准确值并进行比较.

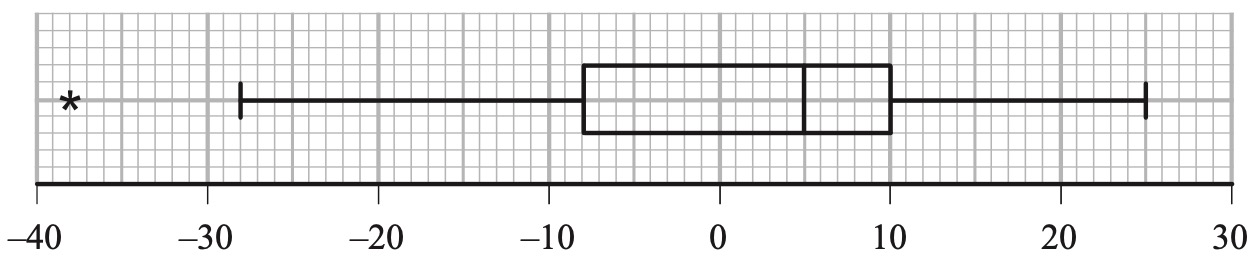
但在部分题目中，问法不够明显，这就要求考生理解两个性质以及在现实生活中的意义. 以下用爱德思（Edexcel）真题举例说明.

Example.

At the start of a course, an instructor asked a group of 80 apprentices to estimate the length of a piece of pipe. The error (true length$-$estimated length) was recorded in centimetres. The results are summarised in the box plot below.

One month later, the instructor asked the 80 apprentices to estimate the length of a different piece of pipe and recorded their errors. The results are summarised in the table below.

Error ($e$ cm)	Number of apprentices
$-40 \lt e \leq -16$	2
$-16 \lt e \leq -8$	18
$-8 \lt e \leq 0$	33
$0 \lt e \leq 8$	14
$8 \lt e \leq 16$	10
$16 \lt e \leq 40$	3

State, giving reasons, whether or not the apprentices’ ability to estimate the length of a piece of pipe has improved over the first month of the course.

本题考察的知识点本质上是比较数据，大部分的考生能够答到中位数更接近$0$，误差减小，所以有提升. 除了集中趋势，还需要考虑波动程度. 波动程度反映的是数据的稳定性，试想一下，如果一组数据的误差是：$-200$、$-100$、$+100$、$+200$，另一组数据的误差是：$-3$、$-2$、$+1$、$+5$，尽管前者的中位数为$0$，但波动程度极大，数据的不稳定会人们怀疑准确性——很有可能前者的猜测比较“幸运”，让最后的平均误差为$0$罢了.

因此，本题还需要答到$\text{IQR}$减少，所以有提升.

知识点拓展：稳定性的好处

在学习离散程度的测量时，我们会将离散程度和稳定性联系在一起，稳定性的提高会提升准确性. 在后续学习中（Edexcel S3；AQA S2；CIE S2），我们会学习概率论中的一个重要定理：中心极限定理（Central Limit Theorem），它指在满足一定条件下，样本均值（Sample Mean）$\overline{X}$的分布近似一个正态分布（Normal Distribution）：

$$ \overline{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right) $$

其中$n$是样本大小（Sample Size）.

现阶段，如果不能理解何为样本均值的分布，不妨考虑这么一个例子，研究人员想估算全国人民的平均年龄，不停地随机抽样（每次随机抽中$n$个人），每一次随机抽样都可以计算出一个平均年龄，并将这些平均年龄记录下来.

平均年龄的数据分布像一个正态分布，而均值是$\mu$（真实的全国人民平均年龄），方差是$\displaystyle \frac{\sigma^2}{n}$（真实的全国人民年龄的方差除以样本大小）.

可以看到，随着样本大小增加，抽样计算出的平均年龄的方差减少，趋近于$0$. 它的好处是，随着样本大小增加，我们单次计算出来的平均年龄会有极大的概率接近真实的平均年龄，也就更加可信.

总结

比较数据是A Level考试中的一类考法，多见于爱德思和CIE考试局. 近年来考察可能性偏低，但考生应该掌握比较角度和描述模版. 有意向进一步学习S系列的考生应加深对离散程度的理解.